Demystifying End-to-End Encryption: A Simplified Introduction to Elliptic-Curve Diffie-Hellman

End-to-end encryption is a critical security measure that ensures only authorized users can access specific information, providing a secure way to transmit data over an unsecured channel, such as the internet. In this context, a “user” can refer to a person or a server.

As society’s concern for security extends to the online environment, it becomes crucial to protect sensitive information from unauthorized access and even from the applications handling the data. End-to-end encryption should be incorporated into all modern applications and websites. This encryption method ensures robust security by fully encrypting communication between individual devices, allowing only the device users with the decryption keys to read the encrypted data. One popular example is WhatsApp, which offers users the option to verify keys to ensure communication integrity.

A vital aspect of information protection is password handling, where applications store the result of a mathematical function rather than the password itself. Another area where end-to-end encryption should be employed is in chat and social media applications.

In this article, we will discuss the Elliptic-curve Diffie-Hellman (ECDH) encryption method and provide a simplified explanation for non-developers. It’s essential to be aware of how your applications and websites protect users’ data. If you have any questions, please feel free to contact us.

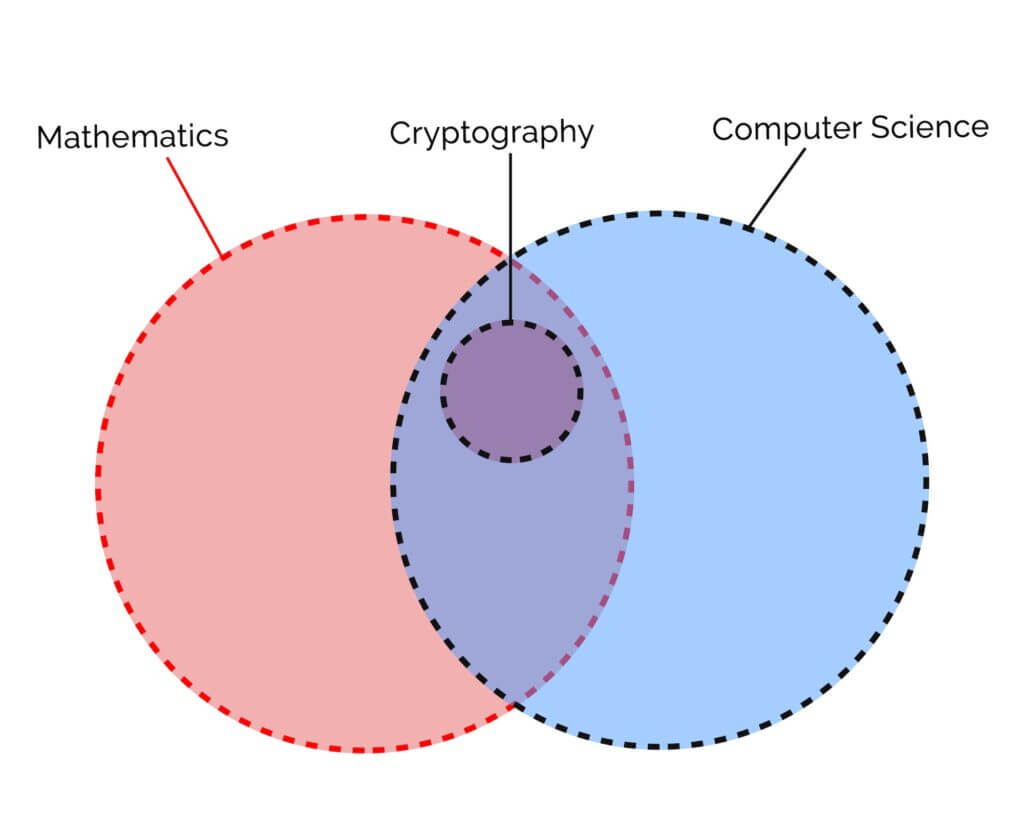
The mathematics of encryption

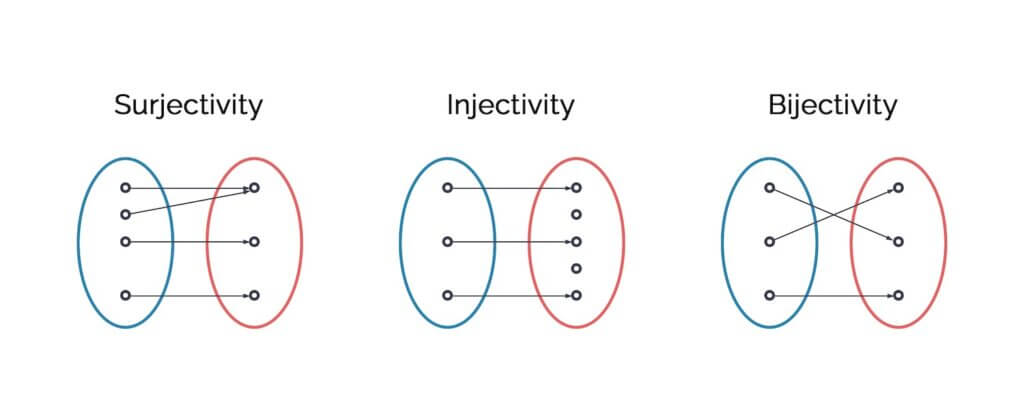
The key to a secure system lies in the functions applied, which possess mathematical properties like injectivity, surjectivity, and bijectivity. Injective and pseudo-injective functions are used to store data when the original data value is not essential, such as in passwords. Bijectivity is crucial when preserving the original information, like in message transmission.

Injectivity is defined as:

a function f:A→B, f(x) ≠f(y) ∀ x,y ∈ A, x ≠ y

Surjectivity is defined as:

a function f:A→B, ∀ y ∈ B ⇒ ∃ x ∈ A, f(x) =y

A function that is both injective and surjective is called bijective, and is described as:

f:A→B, ∀  y ∈ B ⇒∃! x ∈ A, f(x) =y  

Injectivity isn’t a mandatory requirement. In computer science, often, if the probability of an event is low (ex: 1 in 100 mil) it can be treated as non-existent. This can be observed especially when dealing with prime and pseudoprime numbers (https://en.wikipedia.org/wiki/Pseudoprime). There are a lot of fakes in programming.

Surjectivity isn’t important by itself. The critical point however, is whether a function is bijective and bijectivity is related to the existence of an inverse function.

All bijective functions have an inverse. This means that for all bijective functions,

f:A → B, ∃ g: B → A, g(f(x)) =x ∀ x ∈ A

Bijectivity, however, is required when the original information is important. A relevant example of bijectivity is the sending of messages, where the original message is important.

In summary, a secure system depends on applying functions with mathematical properties such as injectivity, surjectivity, and bijectivity. Injective and pseudo-injective functions like passwords are utilized for data storage when the original value isn’t crucial. Conversely, as in message transmission, bijectivity is vital for retaining original information.

Example of end-to-end encryption

A straightforward example of end-to-end encryption involves John and Mary exchanging a secure message, where the message is locked and unlocked using their respective locks and keys:

• John wants to send Mary a message, but doesn’t want anyone else to be able to read it;
• John puts the message into a box, places a lock, then sends the message;
• Mary receives the box, but she can’t get to the message. She places a second lock and sends it back;
• John receives the box, unlocks his lock, and sends it back to Mary;
• Mary unlocks her lock and reads the message.

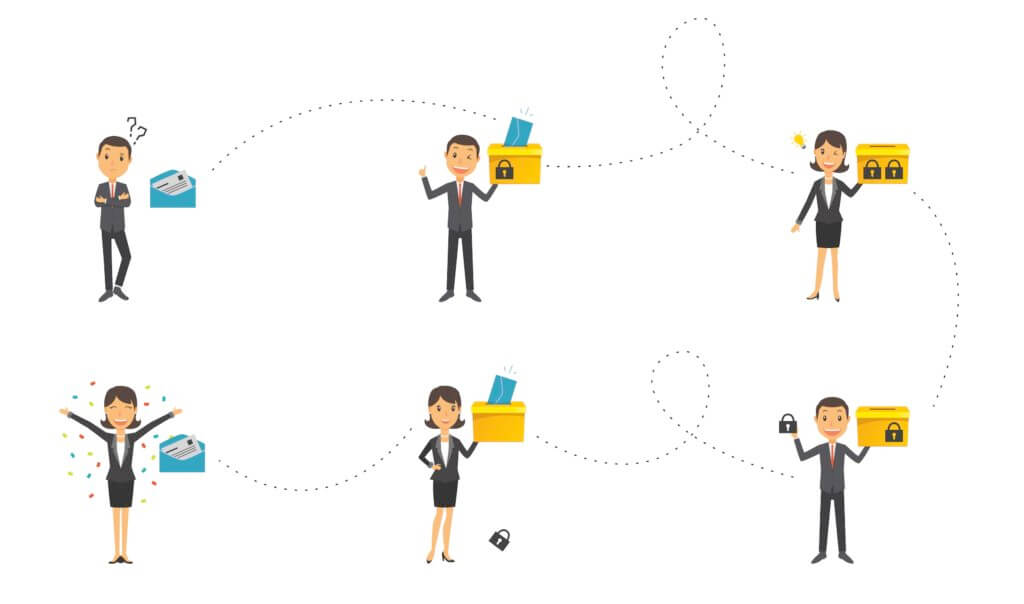
To optimize this process, John and Mary can exchange locks, allowing John to use Mary’s lock to send the message directly.

In computer science, locks and keys are bijective functions inverse to one another:

key(lock(message)) = message

Both key and lock are assigned private and public keys, which are values used to generate the functions:

F(public key) = lock F(private key) = key

Creating a secure system involves finding the function F.

Elliptic-curve Diffie-Hellman (ECDH)

Elliptic-curve Diffie-Hellman (ECDH) is a subset of elliptic curves with a unique property:

F(k1, l2, message) = F(k2, l1, message)

The ECDH algorithm requires the sender’s key and the receiver’s lock to encrypt the message and the receiver’s key and sender’s lock to decrypt it. Since locks are public keys, they can be shared without compromising security. An example of ECDH is the Curve25519.

In practice, no security system is unbeatable. Therefore, keys must be changed periodically. Once you have chosen the function for the algorithm, the next steps involve key exchanges and key resets. Key exchanges require obtaining the receiver’s public key, while key resets occur due to various reasons like key expiration or application restarts. When a key is reset, a new key exchange must take place.

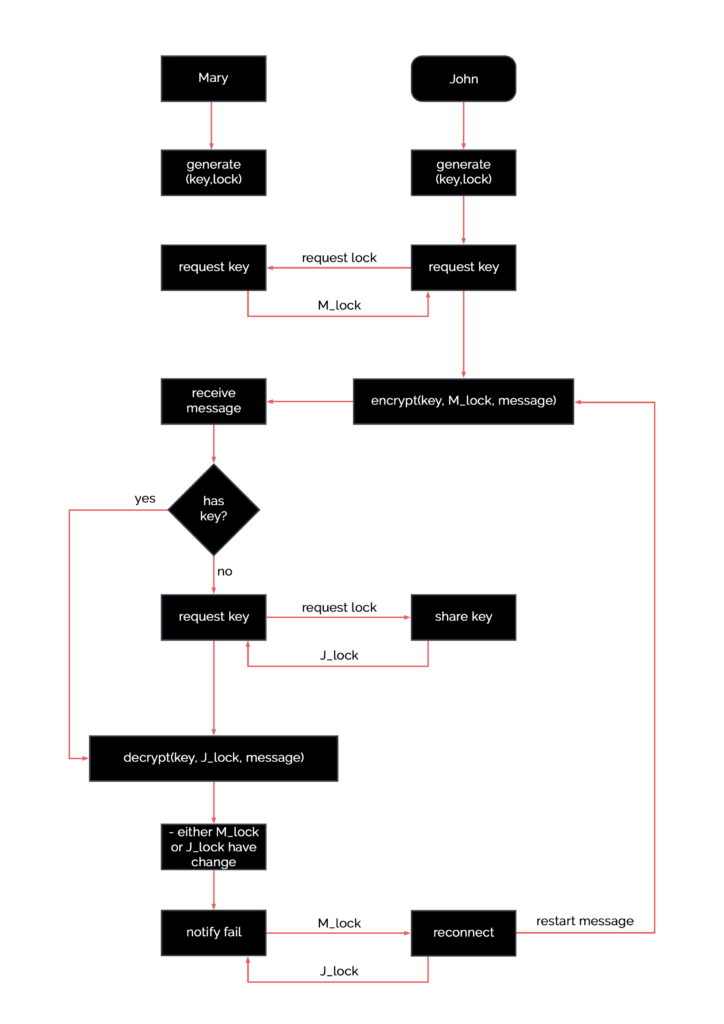
For a visual explanation of the end-to-end encryption algorithm, refer to this diagram below. Note that we’ve also included a key resync algorithm. If you have any questions, we’d be happy to answer them.